Did anybody understand what is an NP problem?

Introduction

This is a fairly complex topic which required me to really look in depth. How I want to structure this post is with explaining some of the fundamentals of Polynomial and Non-deterministic polynomial problems. Then I want to talk about NP Hard and NP Complete problems along with their relationship to each other and finally solve an example question. I will also try to mention some tips on how to address these kinds of problems. Thanks to Abdul Bari youtube videos for amazing explanations.

P and NP Problems

A polynomial-time problem is essentially a problem which can be solved in polynomial time i.e in the worst case scenario it can be solved in O(n^k) time where k is some constant integer. So a lot of the sorting, searching algorithms, and many coding problems we solve are polynomial time problems or fall under the P class. For example

• merge sort is solved in O(nlogn) time
• binary search can be solved in O(logn) time Since logn grows slow compared to n it is a polynomial-time problem.

A problem is a non deterministic problem - if currently we don’t know how to solve it efficiently but can verify it efficiently with a deterministic machine.

Ok what does that mean?

Suppose we have a machine which can only solve problems in O(1) or constant time. We want to do a search algorithm on this machine. The best known search algorithm so far is O(logn). So until we find out a solution for search in O(1) time it becomes a non determinate problem. So if we write down a non determinate algorithm for searching in constant time it would look like this:

def searchConstantTime(searchList, num):
    index = findElement(searchList, num)    # performed in constant time
    if searchList[index]==num:
        return True
    return False

So when we consider a NP problem it is basically non determinate in polynomial time i.e any problem where we have an exponential time complexity and cannot be solved in polynomial time by a polynomial determinate machine it becomes a NP problem. For example if we have to find the subset of a set which sums upto a number S - a classic backtracking problem; the best known algorithm for creating subsets takes 2^n time. (Apologies for my crappy drawing). For each element in the set we have two options and hence it takes O(2^n) time. 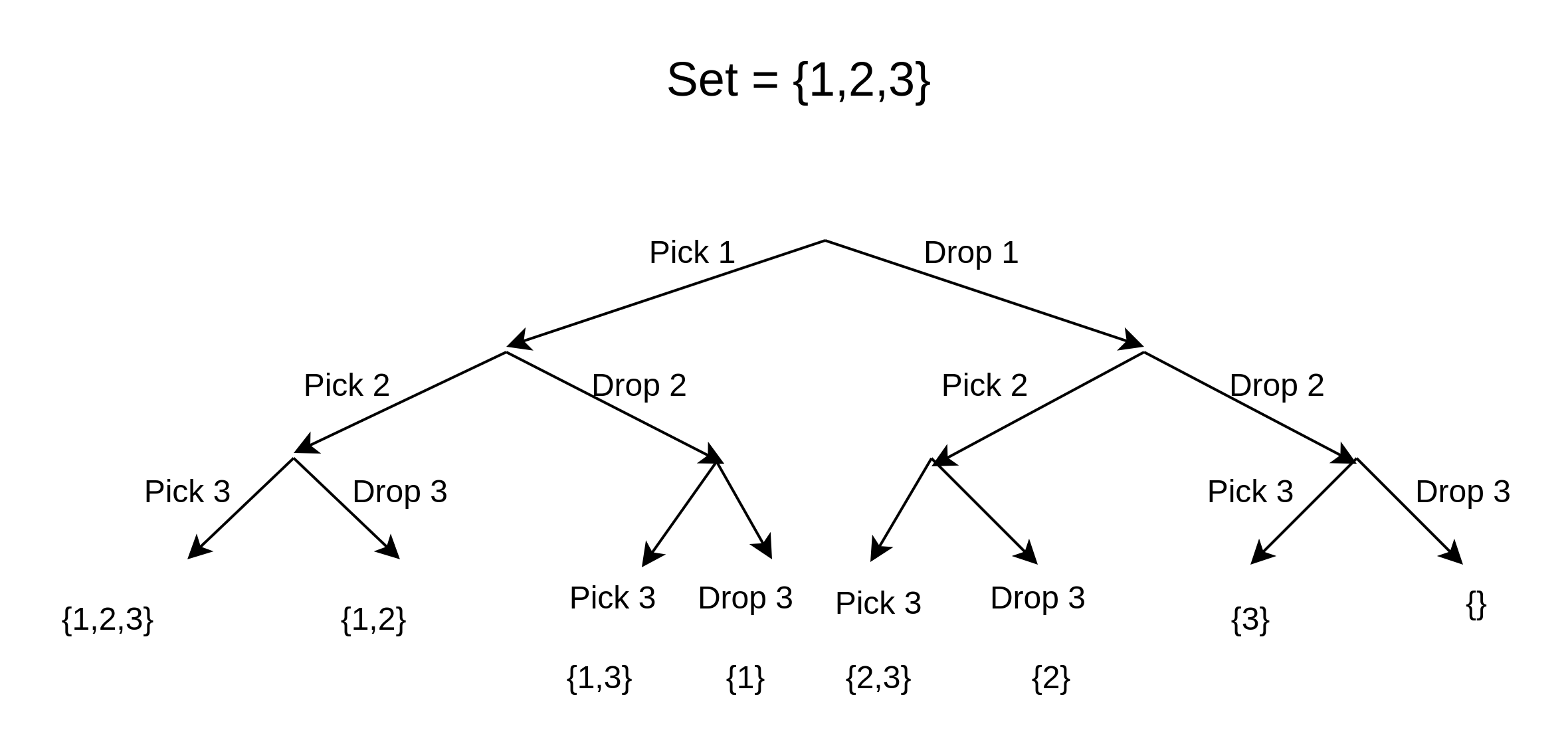So there isn’t any known way to reduce the subset problem to a polynomial problem and until we find a solution for it it will remain a NP problem. Which finally leads to the conclusion that all problems in P class were once in NP class and hence we keep P as a subset of NP. A NP problem will become P when we find a solution for the problem in polynomial time. 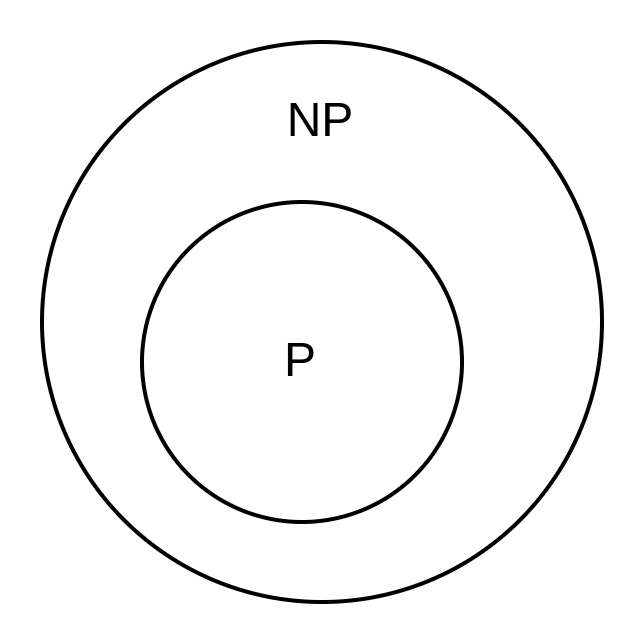An important thing to remember in NP problems is that it can be verified in polynomial time. For example if I say check whether {1,2} is a subset of {1,2,3} which sums to 5, it can be done in O(n) time here which is a polynomial problem.

So takeaway here is P class problems can be solved and verified in polynomial time. NP class problems can be verified in polynomial time.

NP Hard and NP Complete

Okay so the next topic comes NP Hard problems. So where ever I checked they gave a definition like

”A problem is NP hard if it is at least as hard as the hardest problem in NP and if every problem in NP has a polynomial time reduction to the NP Hard problem”.

The word hard is a bit tricky and nuanced to understand; it doesn’t mean it is impossible. So essentially it means - if you solve a NP Hard problem efficiently, you can solve all NP problems. Meaning it is the class of all problems which are atleast as hard as NP problems.

• It may not be verifiable in polynomial time
• No current existing solution to solve a NP hard problem in polynomial time.
• If we can reduce a known NP hard problem to another problem then it also is a NP hard problem.

So the main difference between the class of NP problems and NP-Hard problems is that :

• NP problems have a non deterministic algorithm to solve it; NP Hard doesn’t necessarily have one
• NP problems can be verified in polynomial time, NP Hard problems may not necessarily be verifiable in polynomial time.

As you may have noticed there is a bit of overlap here between NP problems and NP Hard problems. A NP Hard problem which has a known non deterministic algorithm to solve it and can be verified in polynomial time is a NP Complete problem. Here comes the popular diagram!

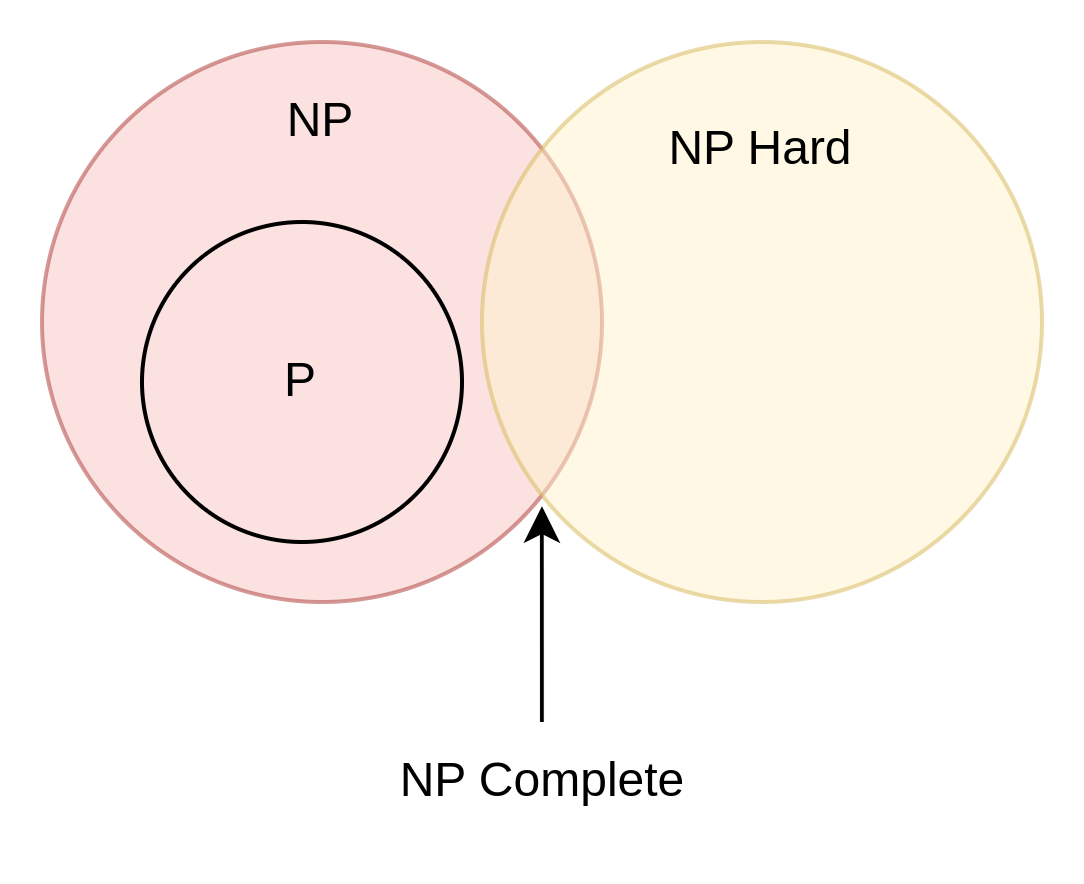
Let’s talk about one problem which is a known NP Hard problem called the Satisfiability problem (SAT). We are given a boolean equation say: a OR b AND c We need to come up with all the combinations of a,b,c which make the equation true.

• To solve this we simply have to create a tree and consider each element.
• At each level we have two options to make the element 0 or 1.

This is just like the subset problem we solved above! The subset problem can basically be reduced to the SAT problem. We can prove this for all problems in NP.

Since we have a non deterministic algorithm to solve SAT now, it is a NP Complete problem. It is actually the first NP complete problem that was discovered.

SAT is a fundamental NP Hard problem because every problem in NP class can be reduced to this problem.

Now that we know that SAT is a NP Hard problem, we can use it as the base for seeing how complex other NP Hard problems are.

So just remember this:

1. If a known NP-Hard problem (like SAT) can be reduced to your problem in polynomial time, then your problem is NP-Hard.
2. And if you can write a non deterministic algorithm for it - it is a NP Complete problem

Cook’s Theorem

Satisfiability is in P if and only if P=NP

Cool theorem right? Satisfiability is the most hard problem in NP. If we ever manage to solve SAT in polynomial time -> it joins P class -> all problems in NP are easier than SAT so NP=P

Proof

1. SAT is NP complete
   • SAT is a NP Problem
   • Every problem L in NP we can reduce L to SAT in polynomial time
2. Assume SAT is a P problem
3. For any problem L in NP there is a polynomial time reduction f for input x such that

x ∈ L ⟺ f(x) ∈ SAT

So here to decide L , it takes polynomial time (since SAT takes polynomial time)

4. Hence

NP ⊆ P

5. We know that

P ⊆ NP

Hence P=NP if we assume SAT is in P

Example with Clique Decision Problem

To determine if a problem is NP Hard, we need to be able to reduce SAT to that particular problem.

So let’s see if Clique Decision problem is a NP Hard problem. We have the following conditions in this problem:

1. A clique is a complete graph i.e. every vertex connects to every other vertex
2. We can say a graph has a clique of size k if the graph contains within it a complete graph of k vertices.

The problem is to find whether a given graph has a clique of size k.

To do this, let us use SAT to construct a graph:

Let us consider k=3 and consider a boolean equation of the form

(A OR B) AND (NOT A OR C) AND (B OR NOT C)

Here we have k clauses where each clause is separated by “AND”. So the equation is

C1 AND C2 AND C3
where C1= (A OR B), C2=(NOT A OR C), C3=(B OR NOT C)

Let us construct a graph with each of these elements and only connect points of different clauses such that they are not the complement of each other i.e.

• we cannot connect A to NOT A and
• we cannot connect points of the same clique.

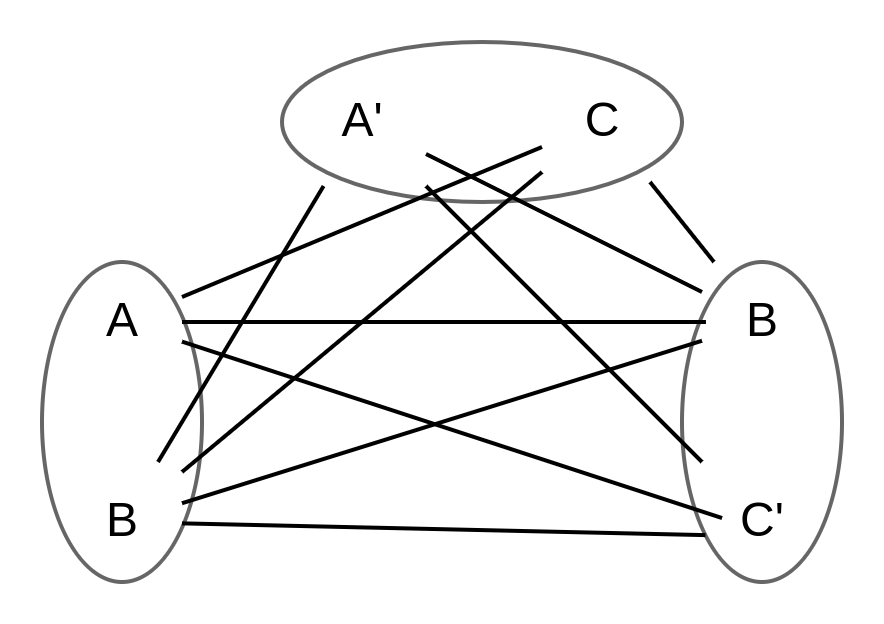
Here we can see that the biggest clique is of size 3, joining B from C1, A’ from C2 and C’ from C3. Coming back to the SAT problem, if we consider this clique and consider the points which we consider to be TRUE then we get the following:

• A’ = 1, B = 1, C’ = 1
• A = 0, B’ = 0, C = 0
• C1 = (A OR B) = (0 OR 1) = 1
• C2 = (NOT A OR C) = (1 OR 0) = 1
• C3= (B OR NOT C) = (1 OR 1) = 1
• C1 AND C2 AND C3 = 1 AND 1 AND 1 = 1

Hence it solves the satisfiability problem. So now we can confirm that solving the Clique Decision Problem is as hard as solving the SAT problem and hence it is a NP Hard solution.

Alright! So hopefully you got something out of that essay - I definitely did :) c u in the next post. k bye.